Article Source

• Title: Life Beyond Column-Stores: Exploiting intra-cycle parallelism
• Authors: Blog from Jignesh Patel’s group @ U. Wisconsin

Life Beyond Column-Stores: Exploiting intra-cycle parallelism

So, I have finally decided to start a blog. Why now, you might ask?

The first reason is that I have been too lazy to start a blog till now. Since blogs often matter as much as publications, this oversight is inexcusable. Better late than never.

The second reason to start a blog is that U. Wisconsin doesn’t, AFAIK, have a blog in the big data space. This is sad given the tradition that our university has in producing key data processing technologies, like the GAMMA parallel database system (which continues to influence what we now call “big data systems”), and BIRCH which provided a key pivot point for data mining (the buzzword-compliant term for that today is “deep data analytics”). This blog is a humble start in trying to get some of what Wisconsin does today in the big data space out into the blogosphere.

So, the topic for today is – Exploiting intra-cycle parallelism for query processing. First, a quick background behind this line of thinking. If you zoom into the processor and view it at the circuit-level, then there is an incredible amount of parallelism within each cycle. For example, if you add two 64-bit numbers, which takes about one cycle, the hardware circuits are actually computing on all the 64 bits in parallel. Thus, there is a 64-way parallelism at the circuit level. Enough here to be a potential game changer if we can exploit it effectively for some key data processing kernel.

The data processing kernel that we picked is a simple scan. Scans are pretty common in practice, and companies like SAP and IBM tend to worry about its efficiency excessively in their main memory data analytics products. Now, if you care about efficiency in these environments, then you should have implemented a column store in your product. So, the real challenge is: How can we speed up scans in a column-store engine?

The answer that Yinan Li and I came up with is called BitWeaving. BitWeaving builds on column stores but takes it to the next level. Here is how it works: First, we take each column and encode it using a fixed-length order-preserving code. So, if you have a column for all the birthdates of users in a table, then we map each unique birthdate in the column to an array of codes (one code for each original column).

Next, we view the codes at the bit-level (just like the processor’s circuit does), and layout the bits in memory in a way that lets us exploit the circuit-level intra-cycle parallelism.

BitWeaving comes in two flavors. The first called BitWeaving/V, is like a column store, but at the bit level.  So, the highest-order bits of the column are layed out sequentially in memory, followed by the second highest-order bit, and so on. Thus, when you bring data into the processor, which is typically about 64-bits at a time, you actually have bits from different columns that are brought into the processor registers.

We have an algebraic framework that allows us to operate on these “oddly packed bits.” With this framework, we can use regular CPU instructions like binary addition and exclusive OR, to operate on bits across the 64 columns in a few instructions (cycles). Furthermore, in many cases, we can safely prune the computation without looking at all the bits! The intuition behind the early pruning is as follows: Consider column codes that are 3-bit wide. If you are evaluating the predicate “col < 2”, then you know that any column with a bit value set to 1 in the most significant bit position does not match the predicate, and you don’t need to look at the last two bits of information. Organizing the column at the bit level allows us toskip over columns of bits. The end result is that in just a few cycles, we can compute the predicate for 64 columns. In other words, we have successfully exploited intra-cycle parallelism!

The second way to BitWeave is called BitWeaving/H. Here we pack the codes horizontally, laying the codes sequentially in memory. Such horizontal code packing is not new, but what we do that is new is:

1. Add an extra bit to each code, which we use as a placeholder to record the result of the predicate evaluation on that code, and 
2. We store consecutive codes stacked as columns across the memory. So, if we have a 3-bit code, the code for column 1 is followed in the memory address space by the code for column 5 (and not column 2!). See the paper more details.

With these techniques we can dramatically reduce the number of cycles that is used by BitWeaving/H to evaluate predicates. The end result is that we can compute the predicate across a batch of codes in a few cycles (again, we have successfully exploited intra-cycle parallelism).

Okay, so how well does this work in practice? Below is a figure comparing the performance of different techniques using cycles/code as the performance metric. These results are for a synthetic data set with a single column and one billion uniformly distributed integer values in this column. In this experiment, we vary the column width (# bits in the code). We scan the table using a predicate that selects 10% of the tuples, and then feed the results to a COUNT aggregate. This experiment was run on a single core of a Xeon X5680.

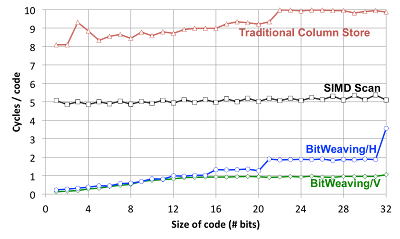The top line in this figure corresponds to fetching one column code at a time, evaluating the predicate, and then feeding the result to a count aggregate operator. The second line labeled “SIMD Scan” is our best effort implementation of the method described in the SAP paper. It packs codes horizontally, like BitWeaving/H, but without the extra bit and the columnar layout, and uses SIMD instructions. The next two lines represent BitWeaving/H and BitWeaving/V.

As we can see, both BitWeaving methods provide significant gains over the traditional method and the SIMD Scan. For example, with a code size of 12 bits, BitWeaving/V is 10X and 6X faster than the Traditional and the SIMD Scan methods respectively. At a code size of 12 bits, BitWeaving/H is 9X and 5X faster than the Traditional and the SIMD Scan methods respectively.

Of course in the experiment above, the final output was a COUNT(*), which can be computed directly by counting how many results match the predicate. As one might imagine BitWeaving/V is more expensive if you have to actually reconstruct the column to produce the output. Here is another experimental result with a TPC-H database at scale factor 10 (i.e. a 10GB database), with the scan query Q6. This query has an aggregate that requires computing the average across a product of two columns.  Here BitWeaving/H outperforms BitWeaving/V.

One final note, BitWeaving can be used both as a native storage format and/or as an index. With 2-way replication, you could choose to store one copy of the column in a BitWeaved format and the other in a regular column store.

Of course, there are lots of interesting unanswered questions, including how to extend this idea of intra-cycle parallelism to work with other columnar compression schemes, expanding the use of BitWeaving beyond simple scans, physical schema optimization using BitWeaving, making BitWeaving work with other architectures (e.g. GPUs), dealing with updates and batch appends, etc. So, we are likely to continue having fun with this line of thinking.