Article Source: REINFORCEMENT LEARNING PART 2: SARSA VS Q-LEARNING
Authors: Travis DeWolf

SARSA vs Q-learning

Main Takeaways

The biggest difference between Q-learning and SARSA is that Q-learning is off-policy, and SARSA is on-policy.

The equations below shows the updated equation for Q-learning and SARSA:

Q-learning:

$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha[r_{t+1}+\gamma \underset{a}{\max} Q(s_{t+1},a)-Q(s_t,a_t)]$

SARSA:

$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha[r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)]$

They look mostly the same except that in Q-learning, we update our Q-function by assuming we are taking action $a$ that maximizes our post-state Q function $Q(s_{t+1},a).$

In SARSA, we use the same policy (i.e epsilon-greedy) that generated the previous action $a_t$ to generate the next action, $a_{t+1}$ which we run through our Q-function for updates, $Q(s_{t+1},a_{t+1}).$ (This is why the algorithm was termed SARSA, State-Action-Reward-State-Action).

Intuitively, SARSA is on-policy because we use the same policy to generate the current action $a_t$ and the next action $a_{t+1}.$ We then evaluate our policy’s action selection, and improve upon it by improving the Q-function estimates.

For Q-learning, we have no constraint on how the next action is selected, only that we have this “optimistic” view that all hence-forth action selections from every state should be optimal, thus we pick the action $a$ that maximizes $Q(s_{t+1},a).$ This means that with Q-learning we can give it data generated by any behaviour policy (expert, random, even bad policies) and it should learn the optimal Q-values given enough data samples.

Source Codes

All the code used is from Terry Stewart’s RL code repository, and can be found both there and in a minimalist version on my own github: SARSA vs Qlearn cliff. To run the code, simply execute the cliff_Q or the cliff_S files.

SARSA stands for State-Action-Reward-State-Action. In SARSA, the agent starts in state 1, performs action 1, and gets a reward (reward 1). Now, it’s in state 2 and performs another action (action 2) and gets the reward from this state (reward 2) before it goes back and updates the value of action 1 performed in state 1. In contrast, in Q-learning the agent starts in state 1, performs action 1 and gets a reward (reward 1), and then looks and sees what the maximum possible reward for an action is in state 2, and uses that to update the action value of performing action 1 in state 1. So the difference is in the way the future reward is found. In Q-learning it’s simply the highest possible action that can be taken from state 2, and in SARSA it’s the value of the actual action that was taken.

This means that SARSA takes into account the control policy by which the agent is moving, and incorporates that into its update of action values, where Q-learning simply assumes that an optimal policy is being followed. This difference can be a little difficult conceptually to tease out at first but with an example will hopefully become clear.

Mouse vs cliff

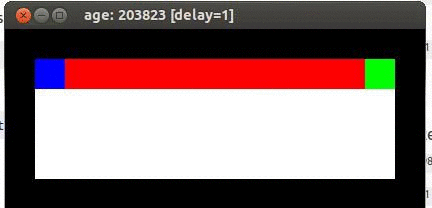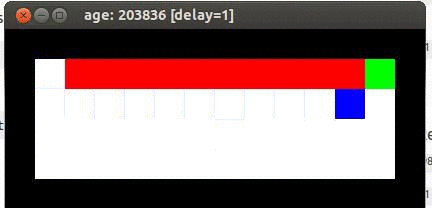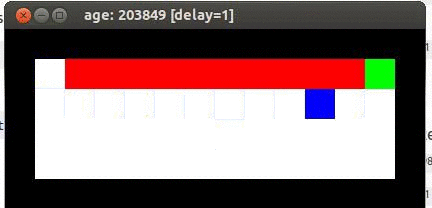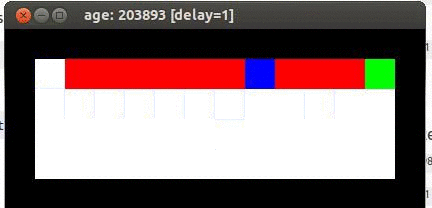
Let’s look at a simple scenario, a mouse is trying to get to a piece of cheese. Additionally, there is a cliff in the map that must be avoided, or the mouse falls, gets a negative reward, and has to start back at the beginning. The simulation looks something like exactly like this:

where the black is the edge of the map (walls), the red is the cliff area, the blue is the mouse and the green is the cheese. As mentioned and linked to above, the code for all of these examples can be found on my github (as a side note: when using the github code remember that you can press the page-up and page-down buttons to speed up and slow down the rate of simulation!)

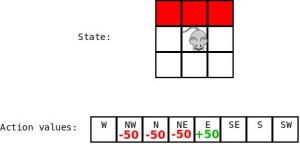
Now, as we all remember, in the basic Q-learning control policy the action to take is chosen by having the highest action value. However, there is also a chance that some random action will be chosen; this is the built-in exploration mechanism of the agent. This means that even if we see this scenario:

There is a chance that that mouse is going to say ‘yes I see the best move, but…the hell with it’ and jump over the edge! All in the name of exploration. This becomes a problem, because if the mouse was following an optimal control strategy, it would simply run right along the edge of the cliff all the way over to the cheese and grab it. Q-learning assumes that the mouse is following the optimal control strategy, so the action values will converge such that the best path is along the cliff. Here’s an animation of the result of running the Q-learning code for a long time:

The solution that the mouse ends up with is running along the edge of the cliff and occasionally jumping off and plummeting to its death.

However, if the agent’s actual control strategy is taken into account when learning, something very different happens. Here is the result of the mouse learning to find its way to the cheese using SARSA:

Why, that’s much better! The mouse has learned that from time to time it does really foolish things, so the best path is not to run along the edge of the cliff straight to the cheese but to get far away from the cliff and then work its way over safely. As you can see, even if a random action is chosen there is little chance of it resulting in death.

Learning action values with SARSA

So now we know how SARSA determines it’s updates to the action values. It’s a very minor difference between the SARSA and Q-learning implementations, but it causes a profound effect.

Here is the Q-learning learn method:

def learn(self, state1, action1, reward, state2):
    maxqnew = max([self.getQ(state2, a) for a in self.actions])
    self.learnQ(state1, action1,
                reward, reward + self.gamma*maxqnew)

And here is the SARSA learn method

def learn(self, state1, action1, reward, state2, action2):
    qnext = self.getQ(state2, action2)
    self.learnQ(state1, action1,
                reward, reward + self.gamma * qnext)

As we can see, the SARSA method takes another parameter, action2, which is the action that was taken by the agent from the second state. This allows the agent to explicitly find the future reward value, qnext, that followed, rather than assuming that the optimal action will be taken and that the largest reward, maxqnew, resulted.

Written out, the Q-learning update policy is Q(s, a) = reward(s) + alpha * max(Q(s')), and the SARSA update policy is Q(s, a) = reward(s) + alpha * Q(s', a'). This is how SARSA is able to take into account the control policy of the agent during learning. It means that information needs to be stored longer before the action values can be updated, but also means that our mouse is going to jump off a cliff much less frequently, which we can probably all agree is a good thing.

Stop Thinking, Just Do!