- Article Source: 시계열 분석 - 모형
- Authors: 푸른생선
Time Series Analysis
시계열(Time Series) 분석을 적용하는 대상
Keywords
- Time
회귀분석은 시점을 고려하지 않지만 시계열 분석은 시간을 고려한다는 점이 가장 큰 차이이다. 이런 차이는 2종 데이터가 존재하지 않더라도 최소한 1개의 데이터와 각 데이터를 획득한 시간을 알고 있다면 결과적으로 2개의 데이터를 가지는 것과 같기 때문에 1종 데이터에 대해서도 자체적으로 분석이 가능해진다.
대표적인 시계열(Time Series) 데이터의 특성과 모형 소개
Keywords
- Autocorrelativeness
- Moving Average
많은 연구자들이 시계열 정보를 크게 2가지로 쪼개어 규칙성을 가지는 패턴과 불규칙한 패턴의 결합이라고 여겨왔다. 따라서, 시계열 모형은 전통적으로 이 두가지를 나누어서 개발되어 왔는데, 규칙성을 만드는 패턴을 또한 두가지로 쪼개어 이전의 결과와 이후의 결과 사이에서 발생하는 자기상관성(Autocorrelativeness)과 이전에 생긴 불규칙한 사건이 이후의 결과에 편향성을 초래하는 이동평균(Moving Average) 현상으로 구분하고 있다. 한편, 많은 수계열 모형들이 불규칙한 패턴을 White Noise라고 칭하고 평균이 0이며 일정한 분산을 지닌 정규분포에서 추출된 임의의 수치라고 규정하고 있는데, 이러한 정규분포 가정은 모델의 해석을 전반적으로 편리하게 만들기 때문에 대부분의 통계 및 수리분석에서 채택되고 있다.
익히 알려진 대표적인 시계열 모델로는 AR모형, MA모형, ARMA모형, ARIMA모형이 있으며, 거의 대부분 시중에 존재하는 모형들은 이러한 기본 모형들의 특수해 또는 개량/변형한 것들에 해당된다. 이 대표모델의 시계열 움직임은 또한 정규분포 성질을 가지기 때문에 해석에서도 여러모로 편리하다.
A. 자기상관(Autocorrelation) - AR모형
자기상관이란 어떠한 Random Variable에 대해서 이전의 값이 이후의 값에 영향을 미치고 있는 상황을 이야기한다. 예를 들면 이전에 값이 크면 이후에는 낮은 값이 나온다거나 하는 경향 따위를 말한다. 이러한 자기상관은 바로 이전의 결과의 영향을 받을 수도 있지만, 드물게는 Delay가 발생하기도 한다. 우리가 실생활에서 가장 많이 발견하는 평균으로 돌아가려는 경향을 지닌 것들이다. 예를 들면 용수철을 원래 길이보다 길게 잡아당기면 이후는 반드시 용수철은 줄어드는 방향으로 반발하는 움직임을 보여 궁극적으로 원래 길이로 돌아가려고 한다.
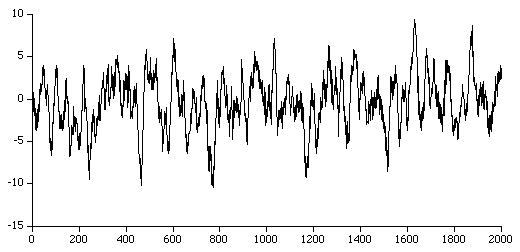
많은 금융정보나 시계열 정보들이 자기상관의 특징을 잘 가지고 있다. 이 데이터는 평균이 0라는 점 외에도 이전에 양수가 나오면 이후에는 음수가 나올 것이다(반대도 가능)는 일정한 패턴도 예상하게 만든다.
자기상관성을 시계열 모형으로 구성한 것을 AR 모형이라고 부르는데, 가장 간단한 형태가 바로 직전 데이터가 다음 데이터에 영향을 준다고 가정한 AR(1) 모형이다.
$ X(t)={aX(t-1)+c}+ue(t)$
좀 쉽게 서술하자면, 시점 $ t$ 에서 얻게 될 $ X(t)$ 의 평균값은 시점 $ t-1$ 에서 얻었던 $ X(t-1)$ 의 값에 $ a$ 를 곱하고 $ c$ 를 더한 것과 같다는 뜻이다. 여기서 $ e(t)$ 항은 white noise라고 부르며 평균이 0이고 분산이 1인 정규분포에서 도출된 random한 값이다. 즉, $ X(t)$ 값은 평균이 $ a*X(t-1)+c$ 이며 분산이 $ u$ 인 정규 분포에서 도출되는 임의의 값이라는 뜻이다.
만약 더 이전의 시점($ P$ 시점)을 모델에 넣고자 하면 $ AR(P)$ 모형이 되는 셈이다.
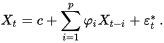
AR(P)모형의 일반식
B. 이동평균(Moving Average) - MA모형
시간이 지날수록 어떠한 Random Variable의 평균값이 지속적으로 증가하거나 감소하는 경향이 생길 수 있다. 예를 들어 봄에서 여름이 될 수록 일반적으로 가계 전기 수요량은 증가하는 경향이 있고 여름에서 겨울로 갈수록 감소하는 경향이 있다. 우리는 특별히 전기세가 크게 부담되지 않는다면 전월의 전기 사용량이 다음월 전기 사용량에 상관을 주지는 않을 것이라고 가정할 수 있고, 아무래도 전기 사용량이 얼마가 될 것인지는 확실히 말하기 어렵기 때문에 이러한 경우 평균이동이 있는 시계열 데이터가 될 것이라고 생각할 수 있다.
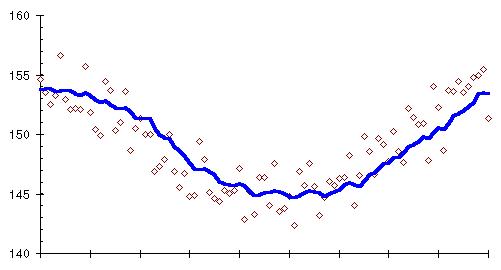
데이터의 평균값 자체가 시간에 따라 변화하는 경향이 Moving Average이다.
이동평균을 시계열 모형으로 구성한 것을 MA 모형이라고 부르는데, 가장 간단한 형태가 바로 직전 데이터가 다음 데이터에 영향을 준다고 가정한 MA(1) 모형이다.
$ X(t)={ae(t-1)+c}+ue(t)$
좀 쉽게 서술하자면, 시점 $ t$ 에서 얻게 될 $ X(t)$ 의 평균값은 시점 $ t-1$ 에서 발생한 error $ e(t-1)$ 의 값에 $ a$ 를 곱하고 $ c$ 를 더한 것과 같다는 뜻이다. 여기서 즉, $ X(t)$ 값은 평균이 $ a*e(t-1)$ 이며 분산이 $ u$ 인 정규 분포에서 도출되는 임의의 값이라는 뜻이다. AR(1) 모형과 가장 결정적인 차이는 이전에 발생한 error가 중요한 것이지 결과적으로 $ X(t-1)$ 이 무엇이였는지는 중요하지 않다는 점이다.
만약 더 이전의 시점($ P$ 시점)을 모델에 넣고자 하면 $ MA(P)$ 모형이 되는 셈이다.
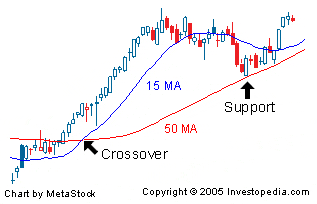
증권가에서 기술적 분석을 할 때 가장 많이 쓰는 것이 MA모형이기도 하다. 예를 들어 최근 50일 평균값보다 최근15일 이동평균값이 커지면 주가가 치솟는다, 즉 골든크로스가 발생한다 같은 접근 말이다.
C. ARMA 모형
ARMA모형은 Autoregressive Moving Average라는 뜻으로, AR모형과 MA모형을 합친 것으로, 연구 기관에서 가장 선호되는 모델이기도 하다. (통상 ARMA(2,2) 정도의 모델이면 충분히 양질의 데이터를 얻는다.)
가장 단순한 형태인 ARMA(1,1) 모형은 아래와 같다.
$ X(t)={aX(t-1)}+{be(t-1)}+c+u*e(t)$
필자가 가장 사랑하는 ARMA(2,2)모형은 아래와 같다.
$ X(t)={a1X(t-1)+a2X(t-2)}+{b1e(t-1)+b2e(t-2)}+c+u*e(t)$
따로 $ ARMA(p,q)$ 모형을 표시하지 않더라도 어떤 형태인지 쉽게 짐작이 되리라 생각한다.
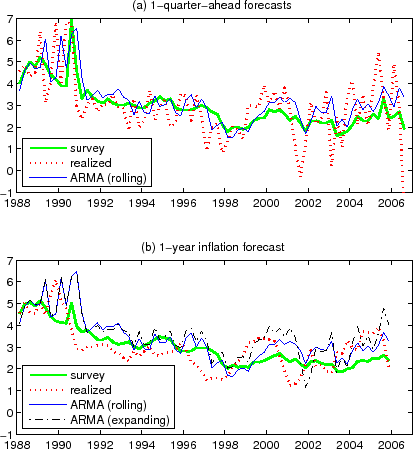
여론조사결과($ X$ )와 실제 발생량의 차이($ e$ )가 가지는 패턴을 이용해서 보다 나은 추정을 할 수 있지 않을까 하는 시도를 해볼 수 있다. 데이터를 보면 여론조사결과 자체보다 ARMA모델의 내삽(interpolation) 결과가 확실히 더 나은 결과를 보이긴 한다. 허나 이 또한 예측력이 그렇게 강해 보이진 않아서 외삽(extraploation)은 시도조차 할 필요가 없어 보인다.
D. ARIMA 모형
Keywords
- Correlation
- Cointegration
- Momentum
ARIMA모형은 Autoregressive Integrated Moving Average라는 뜻으로, ARMA 모형이 과거의 데이터들을 사용하는 것에 반해 ARIMA 모형은 이것을 넘어서서 과거의 데이터가 지니고 있던 ‘추세(Momentum)‘까지 반영하게 된다. 즉, Correlation 뿐 아니라 Cointegration까지 고려한 모델이다.
Cointegration은 Correlation보다 설명하기가 더 어려운데, 가장 단순하게 설명하자고 하면 Correlation은 서로간에 선형관계를 설명하는 것이라면, Cointegration은 추세관계를 설명한다, 즉 cointegration인 시점이 고려되지 않으면 성립하지 않기 때문에 시계열 데이터에만 쓰이는 개념이다.
선형관계
- 두 변수 X-Y간에 correlation이 0보다 크면 X가 큰 값이 나올 때 Y값도 큰 값을 가진다.
- 두 변수 X-Y간에 correlation이 0보다 작으면 X가 큰 값이 나올 때 Y값은 작은 갑을 가진다.
추세관계
- 두 변수 X-Y간에 cointegration이 0보다 크면 X의 값이 이전 값보다 증가하면 Y값도 증가한다.
- 두 변수 X-Y간에 cointegration이 0보다 작으면 X의 값이 이전 값보다 증가하면 Y값은 감소한다.
추가적인 Example
만약 Correlation이 0보다 작고 cointegration은 0보다 큰 관계라면, X가 큰 값이며 증가하는 추세에 있는 경우 Y는 현재 작은 값이나 빠르게 증가하는 추세로 반응하게 된다.
만약 Correlation이 0보다 크고 cointegration은 0보다 작은 관계라면, X가 큰 값이며 증가하는 추세에 있는 경우 Y는 현재 큰 값이나 빠르게 감소하는 추세로 반응하게 된다.
Correlation과 Cointegration의 개념이 다소 혼란스럽겠지만, 간단히 현재의 관계와 추세의 관계라는 요소로 분리해서 생각하다 보면 아주 어렵게 이해되진 않으리라 생각한다. ARIMA 모형은 추세 또한 고려할 수 있기 때문에 momentum을 중요하게 보는 분석가들에게 아주 유용하다.
Note: ARIMA 모델은 자기 자신의 추세만 고려한다. white noise의 추세는 고려하지 않는다. 올바른 모델의 white noise는 추세가 존재하면 안되기 때문이다. 즉, Autoregressive는 자기 자신의 correlation을 말하는 것이고 Integrated 모델은 자기 자신의 cointegration을 말하는 것이다.
결론적으로, 가장 단순한 형태인 ARIMA(1,1,1) 모형은 아래와 같다.
$ a{X(t)-X(t-1)}={bX(t-1)}+{ce(t-1)}+d+ue(t)$
즉 $ X$ 의 추세는 이전 $ X$ 의 값과 이전의 white noise의 결과의 영향을 받게 된다는 뜻이다. 식을 조금 다르게 전개하면 아래와 같은 형태가 된다.
$ X(t)=[X(t-1)+{bX(t-1)}+{ce(t-1)}+d+u*e(t)]/a$
그런데 이 모형은 자세히 보면 ARMA(1,1)과 다를 바가 없다. 그래서, ARIMA(1,1,1)은 사실상 쓰이지 않는다. 그러니 더 복잡한 모델인 ARIMA(1,2,1)를 소개하도록 하겠다.
$ a[{X(t)-X(t-1)}-{X(t-1)-X(t-2)}]={bX(t-1)}+{ce(t-1)}+d+ue(t)$
이는 $ X$ 를 2차 미분한 값에 대한 모델이다. 추세의 추세…라는 표현은 좀 이상하고, 데이터가 확실하게 모멘텀 성향을 지닌다고 가정했을 때 모멘텀의 변화를 모델링한 것이라고 보는 것이 맞겠다. 즉 이 모델은 모멘텀의 변화는 $ X$ 의 이전 값과 이전에 발생한 white noise에 의해 결정된다는 것을 표현한 것이다.
마찬가지로 X(t)에 대해서만 전개하면 아래와 같은 수식이 되며, 이는 사실 ARMA(2,1)과 매우 유사하다.
$ X(t)=(2+b/a)X(t-1)+X(t-2)+(c/a)e(t-1)+(d/a)+(u/a)*e(t)$
수식을 보면서 조금 답답함을 느꼈을 것이고, ARMA모델과 많이 비슷하다는 생각도 했을 것이다.
많은 학자들도 비슷하게 생각하기 때문에 ARIMA 모델을 선호하지 않고 ARMA모델만 택하는 경우도 많으며, 필자 또한 ARIMA 모델을 선호하지 않는다. 특히 추세의 일관성이나 유의미성이 크지 않은 데이터의 경우 ARIMA 모형은 ARMA모형보다 모델의 타당성이 떨어지기도 하다는 점에서 ARIMA 모델을 도입하는 경우가 그리 흔하게 발견되지는 않는 것 같다.