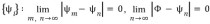Article Source

• An Introduction to Hilbert Spaces
• 힐베르트 공간

An Introduction to Hilbert Spaces

유클리트 공간의 개념을 일반화 한 것으로 존 폰 노이만이 힐베르트의 이름을 따서 만들었다. 2 차원 유클리드 평면과 3차원 공간에서 유한 또는 무한 차원의 공간으로 확장했다. 파동 함수는 힐베르트 공간의 벡터이며 힐베르트 공간은 벡터를 복소 함수로 확장한 공간이다. 힐베르트 공간은 편미분 방정식, 양자역학, 푸리에 분석 등에서 매우 중요하다.

양자 역학에서 계의 물리적 상태는 힐베르트 공간에서 벡터로 나타낸다 - 계의 상태를 나타내는 파동 함수 ψ(x,t) 혹은 스핀 상태 등

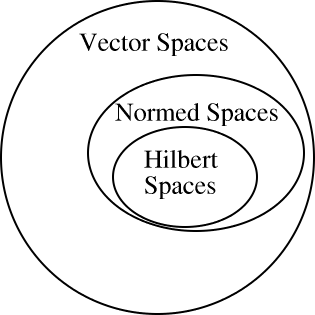
1. 힐베르트 공간은 선형 벡터 공간 (linear vector spaces)이다 - 즉 벡터끼리 서로 더하거나 스칼라로 곱할 수 있는 벡터의 모음을 말하며 벡터를 복소 함수로 확장 한 공간이다.

벡터 더하기

• 만약 벡터 Ψ₁과 Ψ₂ ∈ V라면 Ψ₁ + Ψ₂ ∈ V
• 교환 법칙: Ψ₁ + Ψ₂ = Ψ₂+ Ψ₁
• 결합 법칙: (Ψ₁ + Ψ₂) + Ψ₃ = Ψ₁ + (Ψ₂ + Ψ₃) Ψi + 0 = 0 + Ψi = Ψi
• 역 속성 (inverse property): 벡터 Ψi의 역은 - Ψi 이고 두 개의 벡터를 더하면 0 벡터가 된다. Ψi + (-Ψi) = 0

스칼라 곱

• 만약 벡터 Ψ₁ ∈ V라면 a₁Ψ₁ ∈ V이다. (a₁: 스칼라)
• 분배 법칙: a₁ (Ψ₁+Ψ₂) = a₁Ψ₁ + a₁Ψ₂, (a₁ + a₂)Ψ₁ = a₁Ψ₁ + a₂Ψ₁
• 결합 법칙: a₁(a₂Ψ₁) = (a₁a₂)Ψ₁
• Identity와 0 스칼라 속성: 만약 Ψ₁ ∈ V라면 I 스칼라와 0 스칼라가 존재하며 I·Ψ₁ = Ψ₁·I = Ψ₁이고 0·Ψ₁= Ψ₁·0 = 0 이다.

1. 힐베르트 공간은 내적 연산을 갖는데 다음과 같은 특정 조건을 만족 시켜야 한다.

• 켤레 대칭 (conjugate symmetry): <Ψ₁, Ψ₂> = <Ψ₂, Ψ₁>* 즉 교환 법칙은 불가능하지만 켤레 대칭 한다.
• 2차 벡터 대한 선형: <Ψ₁, aΨ₂, bΨ₃> = a <Ψ₁, Ψ₂> + b <Ψ₁, Ψ₃>
• 1차 벡터에 대한 안티 선형: <aΨ₁ + bΨ₂, Ψ₃> = a<Ψ₁, Ψ₃> + b<Ψ₂, Ψ₃>
• <Ψ, Ψ> = lΨl² ≥0
• 두 벡터 사이의 거리 d = lΨ₂ - Ψ₁l = √(Ψ₂ - Ψ₁, Ψ₂ - Ψ₁)
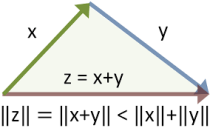
• 삼각 부등식 (triangle inequalty): √<Ψ+ΦlΨ+Φ> ≤ √<ΨlΨ> + √<ΦlΦ>

• Schwarz 부등식: [<ΨlΦ>]² ≤ [<ΨlΨ>][<ΦlΦ>]
• Orthogonality and orthonormality : <ΨlΦ> = 0 --- Ψ와 Φ는 수직, <ΨlΨ> = 1, <ΦlΦ> = 1

1. 힐베르트 공간은 셀 수 있는 복잡한 부분 집합이므로 나눌 수 있다.

2. 힐베르트 공간은 완전하다.

Cauchy Sequence

Introduction to Hilbert Spaces: Important Examples