Article Source

• Overview of Graph Embeddings

---

Overview of Graph Embedding

1. 그래프

그래프는 실생활에서 다양하게 사용되고 있습니다. 소셜 네트워크는 팔로우 관계나 친구 관계를 나타내는 거대한 그래프이고, 생물학자는 단백질의 상호작용을 표현할 때 그래프를 사용하며 통신 네트워크는 그래프 그 자체입니다. 소셜 네트워크에서는 아직 친구 관계가 아니지만 서로 알고 있을 것 같은 사람들을 예측할 수 있고, 생물학자는 분자 구조의 특징을 파악하는 문제를 생각할 수 있습니다. 통신 네트워크에서는 트래픽이 한 곳에 집중되는 문제를 해결하거나 효과적으로 기지국을 설치하는 문제를 풀고 싶을 것입니다.

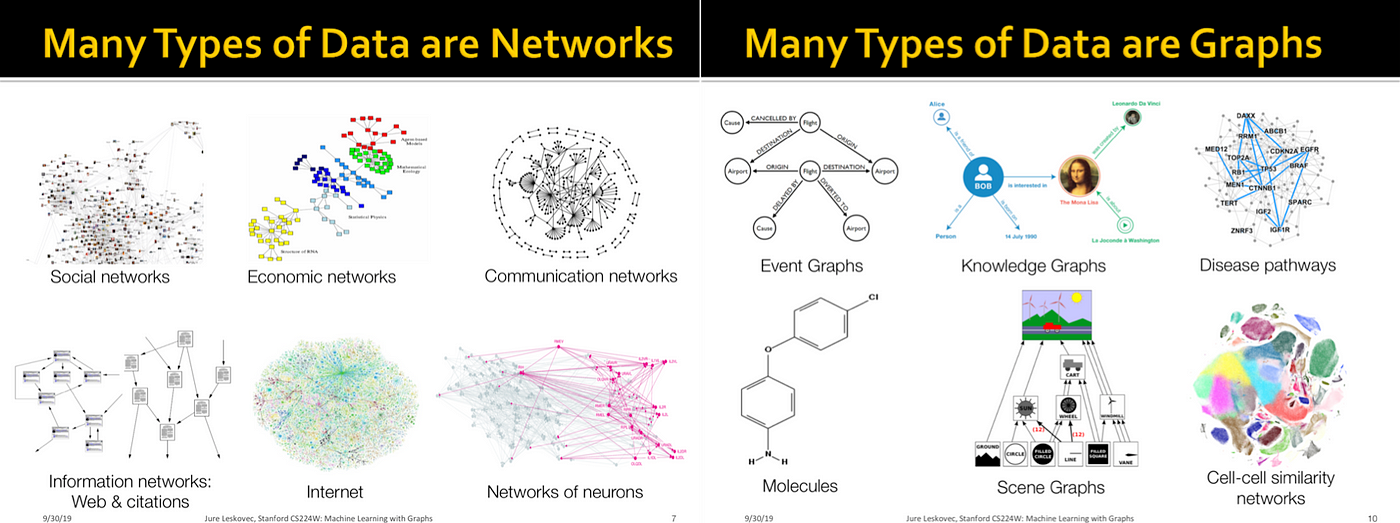
그래프에서의 문제를 단순히 수학적으로, 통계적으로 해결하는 데 그치지 않고 머신러닝 기법들을 적용하는 방법이 계속 시도되고 있습니다. 그래프 임베딩에 대한 연구도 그중 하나로 중요한 역할을 하고 있습니다.

2. 그래프 임베딩이란?

그래프 임베딩은 그래프를 벡터나 벡터 집합으로 변환해주는 것을 말합니다. 아래 그림에서 왼쪽에 있는 그래프의 꼭짓점들을 오른쪽에 있는 2차원 벡터들로 변환할 수 있습니다.

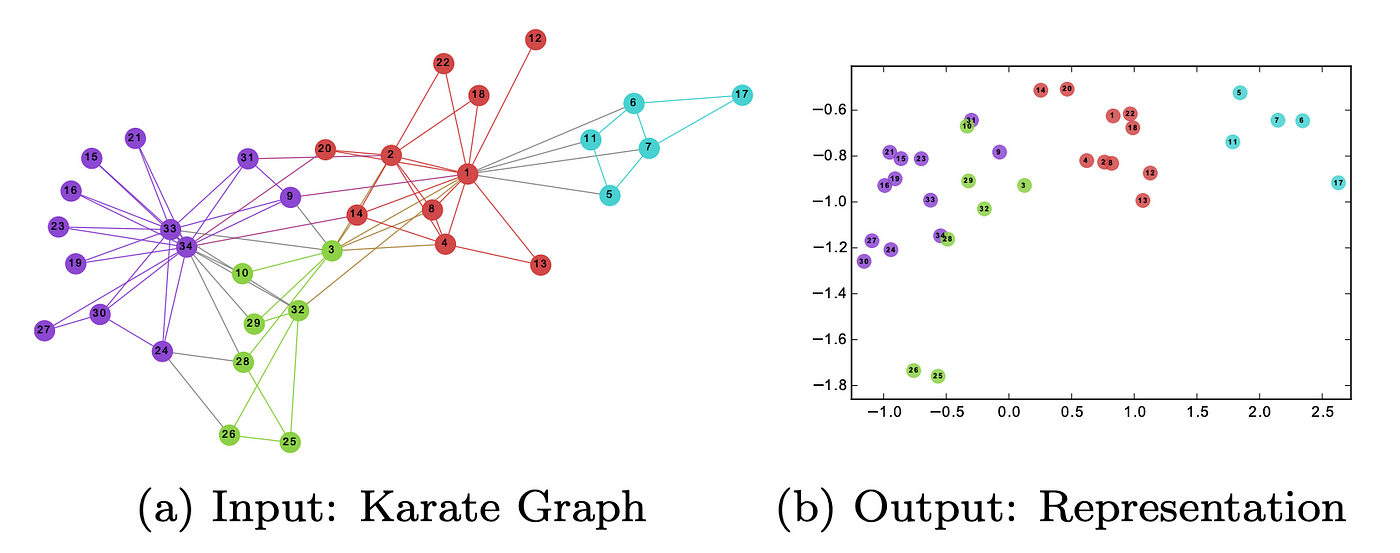
임베딩의 결과는 그래프의 구조, 꼭짓점 간의 관계, 꼭짓점이나 부분그래프와 연관된 다른 기타 부가 정보들을 나타낼 수 있어야 합니다. 다양한 성질을 잘 파악할 수 있도록 여러가지 임베딩 방법들이 계속 연구되고 있습니다. 임베딩은 아래와 같이 크게 두 가지로 나뉩니다.

• [꼭짓점 임베딩: 각 꼭짓점을 벡터로 표현합니다. 꼭짓점 수준에서 예측을 하거나 시각화할 때 사용되는데 좀 더 자세히 말하면 그래프 하나를 평면에 (위의 그림처럼) 시각화하거나 꼭짓점 유사성을 사용해서 새로운 연결을 예측할 때 (페이스북 친구 추천 등) 사용할 수 있습니다.]
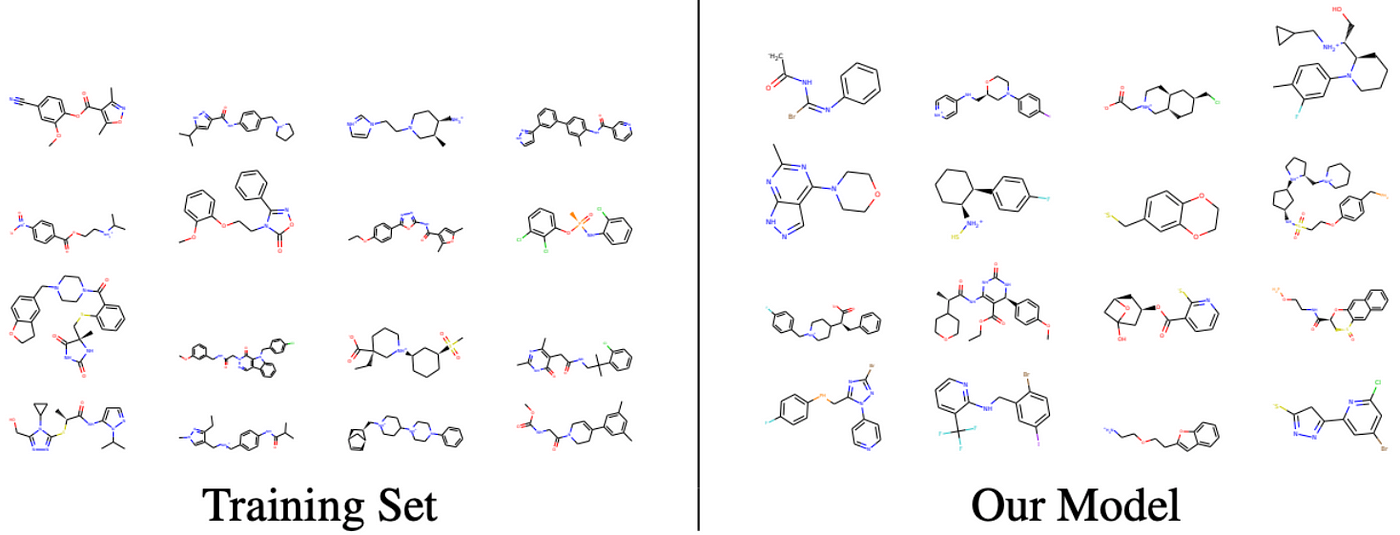
• [그래프 임베딩: 그래프 전체를 벡터로 표현합니다. 그래프 수준(아래 그림이 임베딩으로 나온 결과는 아니지만 ‘그래프 수준’이라는 말을 이해하기에 좋은 그림이라서 첨부했습니다.)에서 예측, 비교, 시각화를 할 때 사용됩니다. 예를 들어, 화학 구조 간의 비교를 생각할 수 있습니다.]

3. 그래프 임베딩을 사용하는 이유

그래프는 그 자체로도 데이터의 의미를 잘 표현하고 있고 사람이 그 의미를 알아보기 쉽다는 장점이 있지만 그럼에도 불구하고 그래프 임베딩이 필요한 이유가 있습니다.

• [그래프에 머신러닝 기법을 직접 적용하는 것은 한계가 있습니다. 그래프는 꼭짓점과 그들을 연결하는 선으로 이루어져 있는데 이것만 사용하기에는 제한이 있습니다. 반면에 그래프를 벡터공간에서 표현해주면 이미 연구된 결과를 가지고 더 다양한 시도를 해볼 수 있습니다.]
• [임베딩은 압축된 표현이라서 공간 효율이 좋습니다. 그래프의 꼭짓점의 개수를 N이라고 할 때, (각 행과 각 열이 꼭짓점을 나타내고 0이 아닌 값은 연결되어있음을 의미하는) 인접행렬(adjacency matrix)의 크기는 N×N 입니다. 그래프가 크면 이 행렬을 다른 알고리즘에 직접 사용하는 건 사실상 불가능합니다. 반면에 그래프를 정해진 차원에 임베딩하면 인접행렬에 비해 훨씬 공간 절약을 할 수 있습니다. 예를 들어, 꼭짓점이 1만 개인 그래프를 20차원에 임베딩한다고 생각하면, 인접행렬의 크기는 1억이고 임베딩 결과의 크기는 20만입니다.]
• [그래프에서 비교 연산을 하는 것보다 벡터 연산이 더 간단하고 더 빠릅니다.]

4. 도전 과제

임베딩을 통해 얻은 결과물은 만족시켜야할 필수요건들이 있습니다. 그 중 대표적인 세 가지를 설명하겠습니다.

• [임베딩이 그래프의 성질을 잘 나타낸다고 확신할 수 있어야 합니다. 그래프의 연결상태, 주변구조 등을 잘 표현하고 있어야 합니다. 임베딩을 사용한 시각화나 예측의 성능은 임베딩 자체 성능에 특히 큰 영향을 받기 때문입니다.]
• [그래프의 크기가 임베딩하는 속도에 주는 영향이 작아야 합니다. 소셜 네트워크를 생각하면 알 수 있듯이 일반적으로 다뤄지는 그래프는 엄청 큽니다. 큰 그래프를 효율적으로 다룰 수 있는 방법은 좋은 임베딩 방법의 필수요소입니다.]
• [가장 큰 어려움은 임베딩 차원을 결정하는 것입니다. 차원을 늘리면 많은 정보를 담을 수는 있지만 성능의 증가에 비해 알고리즘의 시간복잡도나 공간복잡도가 크게 증가합니다. 장단점 중에 어떤 요소를 얼마나 택할지는 사용자가 직접 정해야 합니다. 대부분 논문의 결과를 보면 주로 128이나 256 정도면 충분하다고 합니다. 참고로 (다음에 나올) word2vec 방법에선 300을 사용했습니다.]

5. Word2vec

그래프 임베딩 방법에 대해 설명하기 전에 자연어처리에서의 연구결과인 word2vec과 skip-gram에 대해 먼저 설명을 하겠습니다. 이 두 방법을 알아야 뒤에서 설명할 그래프 임베딩 방법을 이해할 수 있습니다. 더 많이 공부하고 싶으면 튜토리얼과 동영상을 보시길 바랍니다.

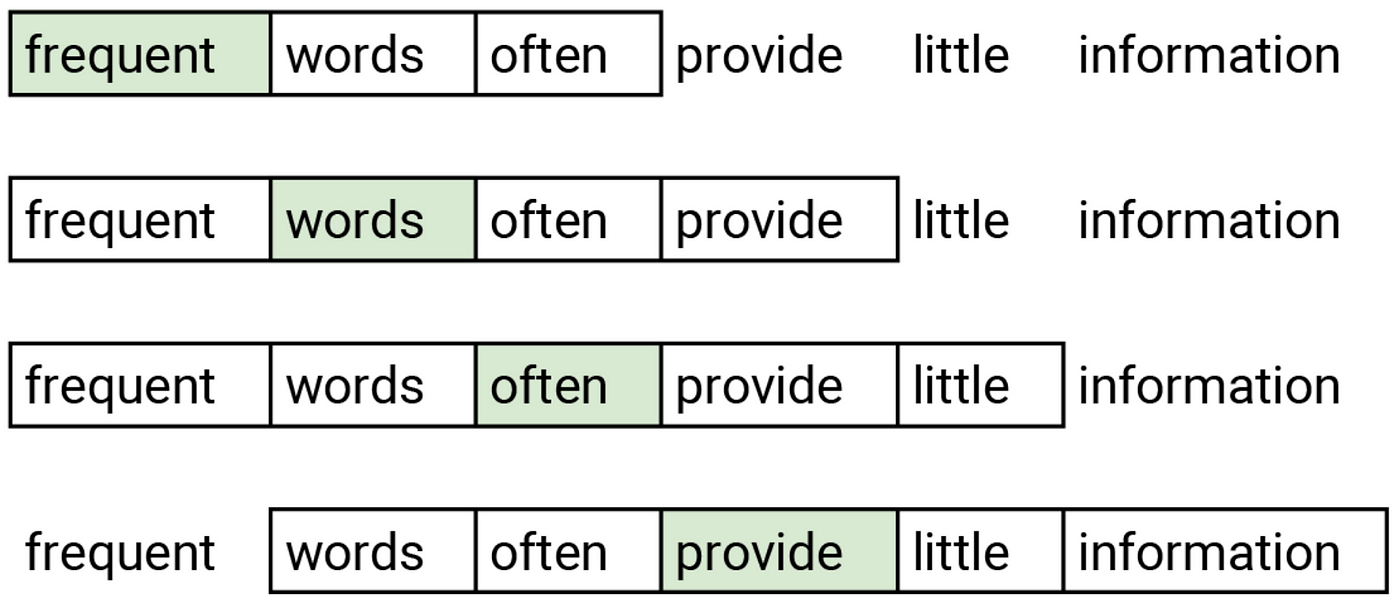
Word2vec은 단어를 벡터로 변환하는 임베딩 방법입니다. 비슷한 단어들은 비슷한 임베딩들로 변환되어야 합니다. Word2vec은 한 층으로 이뤄진 skip-gram 신경망을 사용합니다. Skip-gram은 문장에서 근처에 있는 단어를 예측하기 위해 학습이 됩니다. 이 작업은 가짜 작업이라고 부르는데 학습 단계에서만 사용되기 때문입니다. 신경망은 단어를 입력값으로 받고 근처에 있는 단어를 높은 확률로 예측하도록 최적화됩니다. 위 그림은 초록색 입력 단어와 근처(두 단어 앞/뒤)에 있는 단어 즉, 예측할 단어가 뭔지 보여줍니다. 비슷한 의미를 갖는 단어들은 근처에 있는 단어들이 비슷하기 때문에 이 작업을 통해 비슷한 단어는 비슷한 임베딩을 갖게 해줄 수 있습니다.

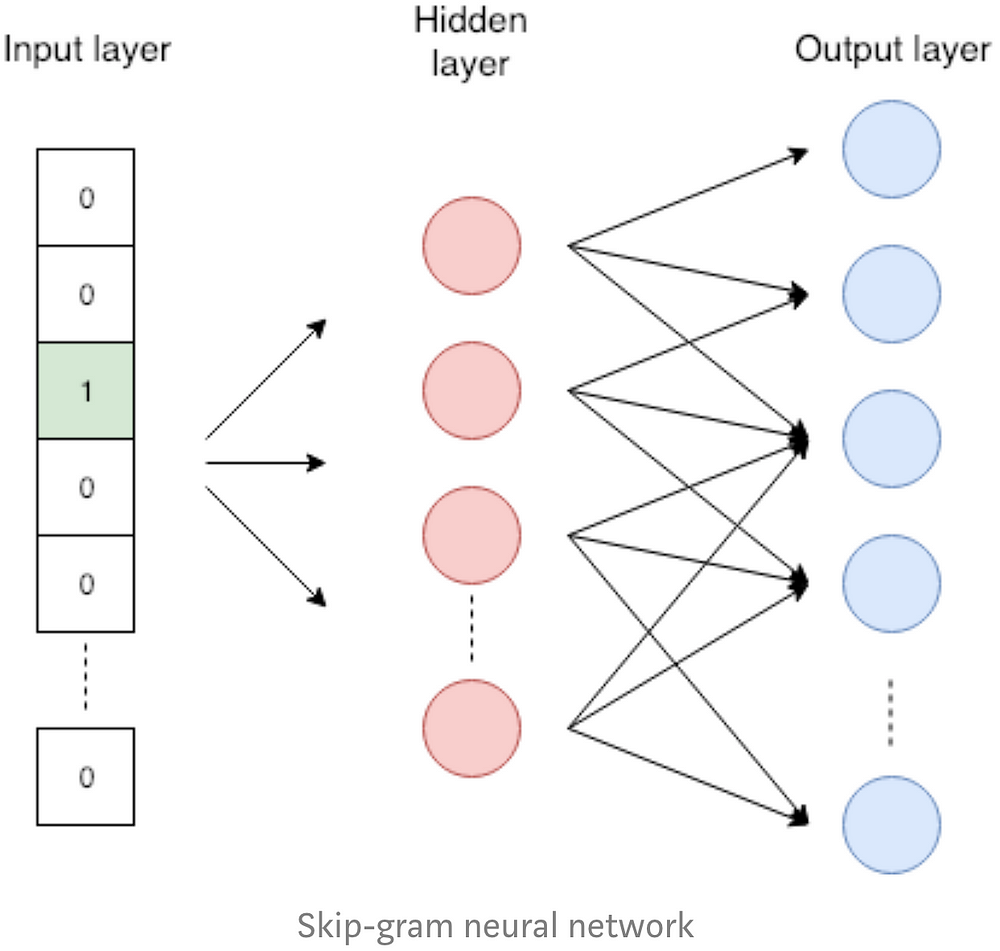
Skip-gram 신경망은 왼쪽 그림처럼 입력층, 은닉층(hidden-layer) 한 개, 출력층으로 이루어져 있습니다. 단어를 입력층에 넣을 때 원-핫 인코딩된 벡터를 사용합니다. 이 벡터의 길이는 단어 사전 크기와 같고 해당 단어에 해당하는 좌표는 1로, 나머지는 0으로 이루어져 있습니다. 은닉층에는 활성화 함수가 없고 결과값이 단어의 임베딩 결과가 됩니다. 출력층에선 소프트맥스 분류기(softmax classifier)를 통해 근처 단어를 예측합니다. 위에서 소개한 튜토리얼에서 각 단계별로 자세한 과정을 확인할 수 있습니다.

6. 그래프 임베딩 방법들

실제로도 자주 쓰이고 일반적으로 좋은 성능을 보이는 그래프 임베딩 방법 네 개를 소개하려고 합니다. 앞 세 개(DeepWalk, node2vec, SDNE)는 그래프의 꼭짓점을 벡터로 변환하는 꼭짓점 임베딩이고 나머지(Graph2vec)는 그래프 하나를 하나의 벡터로 바꾸는 그래프 임베딩입니다.

6-1. DeepWalk

DeepWalk는 랜덤 워크(random walk)를 사용해서 임베딩을 생성합니다. 랜덤 워크는 말그대로 꼭짓점 위를 임의로 걸어다니는 것을 말합니다. 한 꼭짓점에서 시작해서 임의의 이웃으로 가고 또 그 꼭짓점의 임의의 이웃으로 정해진 횟수만큼 이동합니다. 이렇게 이동했을 때 방문한 꼭짓점들의 나열한 것을 랜덤 워크라고 합니다. DeepWalk는 아래 세 단계로 구성됩니다.

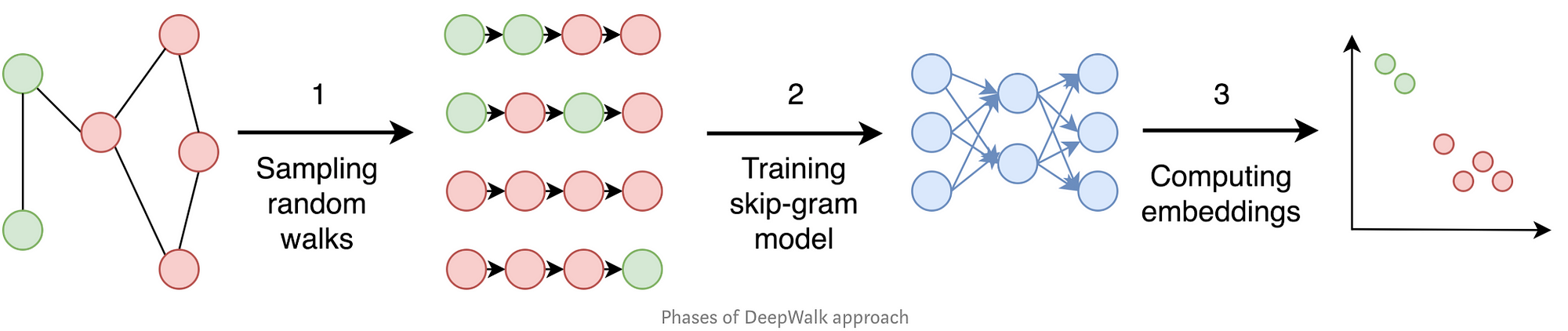
• [샘플링: 입력된 그래프에서 랜덤 워크를 샘플링합니다. 각 꼭짓점에서 출발하는 랜덤 워크를 여러 개씩 생성합니다. 논문에서는 각 노드별로 랜덤 워크를 32~64개씩 만들고 랜덤 워크의 길이는 약 40이 좋다고 합니다.]
• [Skip-gram 학습: 위에서 생성된 랜덤 위크는 word2vec에서 문장에 대응됩니다. Skip-gram 신경망은 원-핫 인코딩된 꼭짓점 벡터을 입력으로 받고 근처에 있는 꼭짓점을 잘 예측하도록 학습합니다. 이 때, 앞뒤로 꼭짓점 10개를 봅니다.]
• [임베딩 계산: 임베딩으로 위 신경망에서 은닉층의 출력값을 씁니다. DeepWalk는 주어진 그래프의 모든 꼭짓점의 임베딩을 계산합니다.]

DeepWalk는 랜덤 워크를 임의로 만들기 때문에 각각의 랜덤 워크에서 앞뒤를 잘 파악했더라도 원래 그래프로 돌아왔을 때 꼭짓점의 주변 이웃을 잘 파악하지 못할 수 있다는 단점이 있습니다. 다음에 나오는 node2vec에서 그 점을 보완합니다.

6-2. Node2vec

Node2vec은 DeepWalk에서 랜덤 워크를 생성하는 방법을 발전시킨 방법입니다. 대략 설명하면 파라미터 p, q가 있는데, 랜덤 워크를 만들 때 p는 직전 꼭짓점으로 돌아올 가능성을 조절하고 q는 직전 꼭짓점으로부터 얼마나 멀어질지를 조절합니다. 즉, p는 주변을 얼마나 잘 탐색하는지에 대한 파라미터이고 q는 랜덤 워크가 얼마나 새로운 곳을 잘 발견하고 탐색하는지에 대한 파라미터입니다.

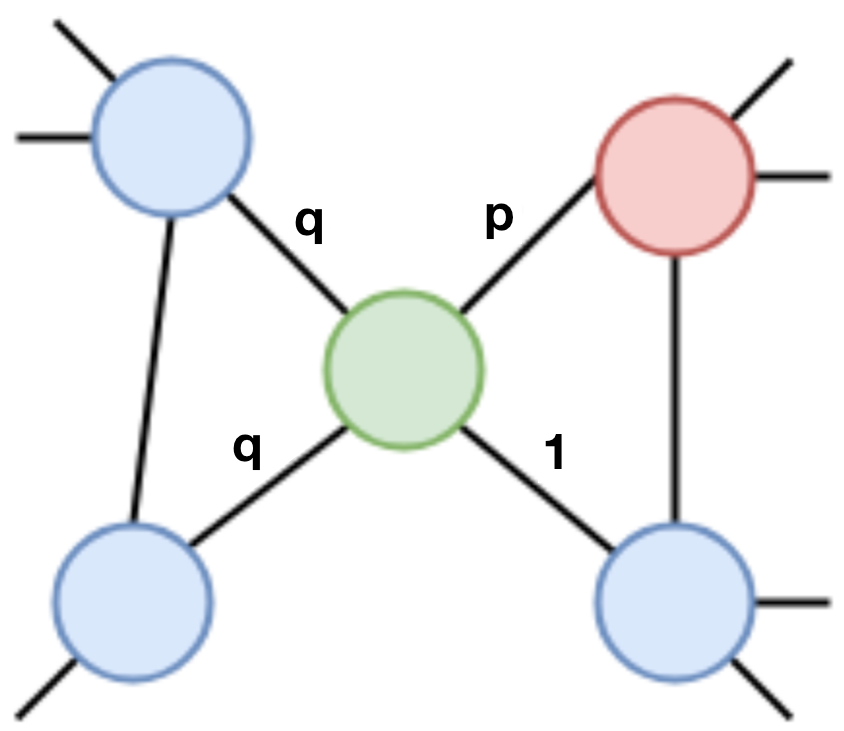
왼쪽 그래프에서 랜덤 워크가 진행 중인데 빨간색 꼭짓점에서 초록색 꼭짓점으로 넘어온 상황을 생각해봅시다. 다시 빨간색으로 돌아올 확률은 p/(p+2q+1), 빨간색과 초록색의 공통 이웃으로 움직일 확률은 1/(p+2q+1), 빨간색으로부터 더 멀어질 확률은 2*(q/(p+2q+1))로 랜덤 워크가 진행됩니다. p와 q를 조절해서 목적에 맞는 임베딩을 찾을 수 있습니다. 다른 단계(skip-gram 학습, 임베딩 계산)는 deepWalk와 같고 따라서, p=q=1인 경우의 node2vec은 deepWalk와 같습니다.

6-3. SDNE

SDNE(Structural Deep Network Embedding)는 랜덤 워크를 쓰지 않기 때문에 위 두 방법과는 크게 다른 방법입니다. 이 방법을 소개하는 이유는 다양한 영역에서 성능이 안정적이기 때문입니다. SDNE의 장점은 한 단계 이웃관계과 두 단계 이웃관계를 잘 반영한다는 것인데 각각의 의미는 아래와 같습니다.

• [한 단계 이웃관계는 연결된 두 꼭짓점 간의 비슷한 정도를 즉, 상대적으로 좁은 관계를 의미합니다. 어떤 논문이 다른 논문을 인용했다면 비슷한 내용을 다뤘다는 것을 의미하듯이 두 꼭짓점이 연결되어 있으면 두 꼭짓점의 임베딩은 서로 비슷해야 합니다.]
• [두 단계 이웃관계는 각 꼭짓점의 주변 구조가 얼마나 비슷한지를 즉, 상대적으로 넓은 관계를 의미합니다. 지수가 킬링 이브, 스캄 프랑스, 리틀 드러머 걸을 좋아하고 지은이가 킬링 이브, 스캄 프랑스, 체르노빌을 좋아하면 (많이 겹쳤다고 가정하자.) 둘의 취향은 비슷할 가능성이 높습니다.]

그래프의 인접행렬의 한 행을, 그 행에 대응되는 꼭짓점의 인접벡터라고 부르는데 정의에 의해 이웃한 꼭짓점들에 해당하는 좌표의 값이 1이고 나머지는 0인 벡터가 됩니다. 꼭짓점의 인접벡터가 아래 그림에 나오는 오토인코더의 입력값입니다. 이 오토인코더를 바닐라 오토인코더라고 부르는데 두 단계 이웃관계를 학습하게 됩니다.

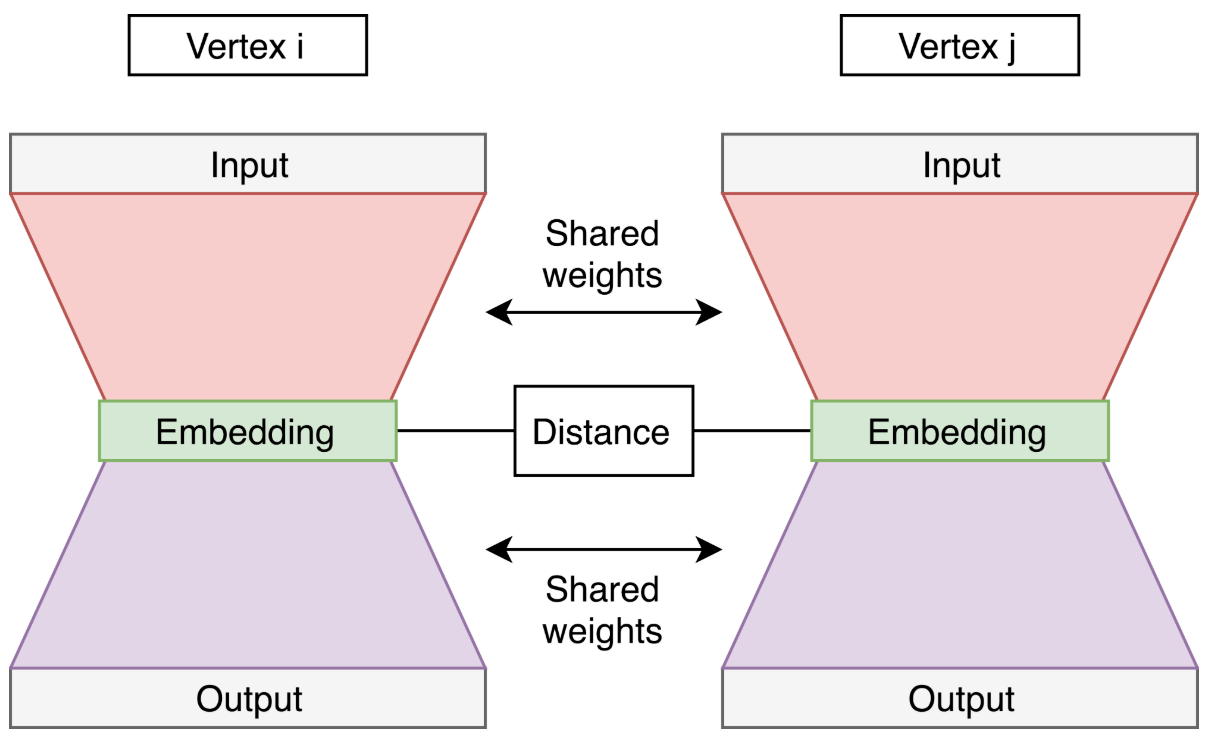
양쪽(그림에서 오른쪽과 왼쪽)에서 나온 임베딩의 거리를 계산하고 이 값을 신경망의 손실함수에 포함합니다. 선으로 연결된 모든 두 꼭짓점쌍에 대해 거리를 계산하여 더함으로써 모델이 한 단계 이웃관계를 잘 표현할 수 있게 됩니다.

SDNE 모델의 전체 손실함수를 오토인코더의 손실함수와 위에서 계산한 거리를 더한 값으로 정해서 SDNE가 한 단계 이웃관계과 두 단계 이웃관계를 모두 잘 표현할 수 있도록 합니다.

6-4. Graph2vec

마지막으로 소개할 방법은 그래프 전체를 벡터로 변환하는 것입니다. 즉, 벡터 하나가 그래프 전체를 묘사합니다. 지금까지 나온 방법 중 성능이 가장 좋은 graph2vec를 소개하겠습니다.

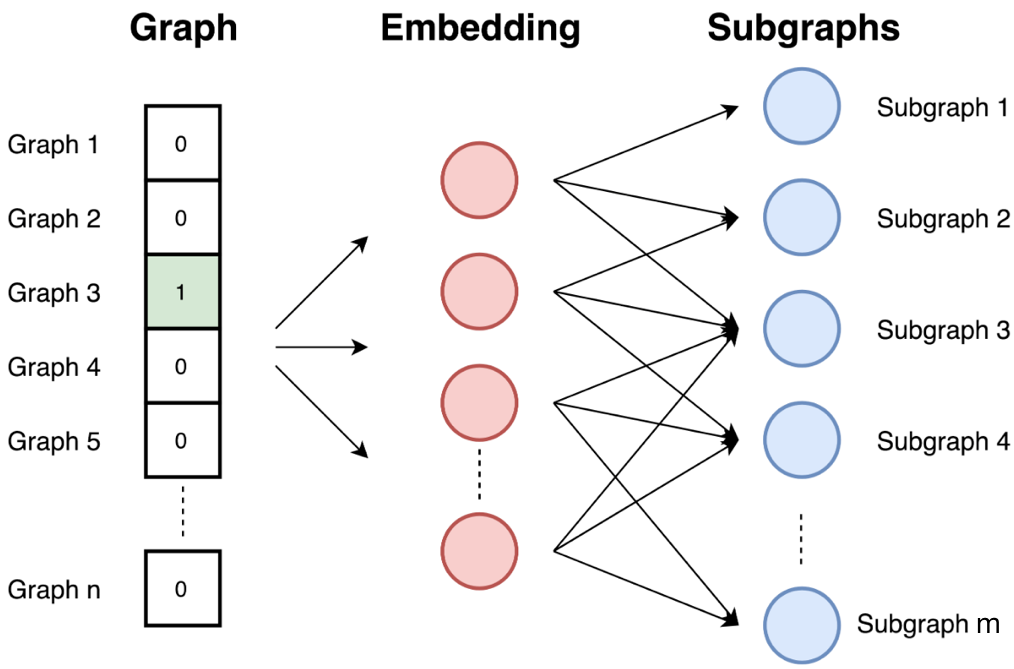
Graph2vec은 doc2vec이 skip-gram을 사용한 아이디어를 기초로 합니다. 간단히 요약하면, 문서(document)의 아이디를 입력값으로 받고 문서에 포함된 단어를 예측하기 위한 학습을 하는 방법입니다. 자세한 설명은 이 글을 참조하길 바랍니다. Graph2vec은 아래 세 단계로 구성됩니다. (위에 있는 그림 참고)

• [그래프의 모든 뿌리가 있는 부분그래프(rooted subgraphs)를 샘플링하고 레이블을 다시 지정합니다. 그 결과로 위 그림에서 m개의 subgraph를 얻습니다. 여기에서 뿌리가 있는 부분그래프는 특정 꼭짓점(뿌리)을 중심으로 정해진 거리 안에 있는 꼭짓점의 집합입니다.]
• [skip-gram 모델을 학습합니다. 문서는 단어(혹은 문장)의 집합이고 그래프는 부분그래프의 집합이기 때문에 그래프를 문서와 비슷하게 볼 수 있습니다. 이런 관점으로 입력된 그래프에 부분그래프가 있을 확률을 계산하는 skip-gram 모델을 학습합니다. 입력 그래프는 원-핫 인코딩된 벡터의 형태로 들어옵니다.]
• [그래프의 아이디가 원-핫 인코딩 되어 들어오면 임베딩을 계산합니다. DeepWalk와 마찬가지로 은닉층의 결과가 임베딩이 됩니다.]

모델이 부분그래프를 예측하도록 설계되어있기 때문에 두 그래프가 비슷한 부분그래프를 가지면, 즉 비슷한 구조를 가지면 비슷한 임베딩이 나오게 됩니다.

7. 다른 방법들

더 관심 있는 분들을 위해 다른 모델들을 소개하며 글을 마칩니다.

• [꼭짓점 임베딩 방법: LLE, Laplacian Eigenmaps, Graph Factorization, GraRep, HOPE, DNGR, GCN, LINE]
• [그래프 임베딩 방법: Patchy-san, sub2vec, (Deep) WL kernels]

8. 참고자료

[1] C. Manning, R. Socher, Lecture 2 | Word Vector Representations: word2vec (2017).

[2] B. Perozzi, R. Al-Rfou, S. Skiena, DeepWalk: Online Learning of Social Representations(2014).

[3] C. McCormick. Word2Vec Tutorial — The Skip-Gram Model(2016).

[4] T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space (2013).

[5] A. Narayanan, M. Chandramohan, R. Venkatesan, L. Chen, Y. Liu, S. Jaiswal, graph2vec: Learning Distributed Representations of Graphs(2017).

[6] P. Goyal, E. Ferrara, Graph Embedding Techniques, Applications, and Performance: A Survey(2018).

[7] D. Wang, P. Cui, W. Zhu, Structural Deep Network Embedding (2016).

[8] A. Grover, J. Leskovec, node2vec: Scalable Feature Learning for Networks (2016).